第7章 GNNのスケーラビリティ

はじめに

グラフニューラルネットワークは，大規模なグラフへの適用が難しいという深刻な拡張性（スケーラビリティ）の問題を抱えている，例として，ノード分類問題にGCNフィルタベースのモデルを用いることを考える．このとき，以下の損失関数を最小化するのに勾配降下法を用いる（下記式はと同じであり，GNNをGCNに書き換えている）：

\[\tag{7.1} \mathcal{L}_{\text{train}}=\sum_{v_i \in \mathcal{V}_l} \ell\left(f_{\text{GCN}}(\symbf{A}, \symbf{F} ; \symbf{\Theta})_i, y_i\right)\]

ここで， $\ell(\cdot)$ は損失関数である． $f_{\text{GCN}}(\symbf{A}, \symbf{F} ; \symbf{\Theta})$ は以下のような $L$ 層のGCNフィルタ層からなる：

\[\tag{7.2} \symbf{F}^{(l)}=\hat{\symbf{A}} \symbf{F}^{(l-1)} \symbf{\Theta}^{(l-1)}, \quad l=1, \ldots, L\]

ここで， $\hat{\symbf{A}}$ は $\widetilde{\symbf{D}}^{-\frac{1}{2}} \widetilde{\symbf{A}} \widetilde{\symbf{D}}^{-\frac{1}{2}}$ を表し， $\symbf{F}^{(0)}=\symbf{F}$ である．簡単のため，ノード表現はすべての層で同じ次元 $d$ を持つとする．グラフフィルタ層の間に活性化関数を入れることもできるが，この定式化では無視している．また，式(7.1)のパラメータ $\symbf{\Theta}$ は $\symbf{\Theta}^{(l)}$ のように各層のモデルパラメータで構成される( $l=1, \ldots, L$ )．

損失関数を最小化する勾配降下法のパラメータ更新は次のように書くことができる：

\[\tag{7.3} \symbf{\Theta} \leftarrow \symbf{\Theta}-\eta \cdot \nabla_{\symbf{\Theta}} \mathcal{L}_{\text {train}}\]

ここで， $\eta$ は学習率を表し，勾配 $\nabla_{\symbf{\Theta}} \mathcal{L}_{\text {train }}$ は全学習データ $\mathcal{V}_l$ 上で評価する必要がある．さらに，式(7.2)に示されるようにGCNフィルタの設計により， $\mathcal{L}_{\text{train}}$ を順方向に評価する際には， $\mathcal{V}$ の全ノードが計算に関与する．これは各層ですべてのノード表現が計算されるためである．したがって，各学習エポックにおける順方向のパスにおいて，すべてのノード表現と各グラフフィルタ層のパラメータをメモリに保持しておく必要がでてくる．グラフが大きくなると，必要なメモリは膨大になってしまう．

具体的に，必要なメモリを計算してみよう．順方向に評価するとき，規格化した隣接行列 $\hat{\symbf{A}}$ ，すべての層のノード表現 $\symbf{F}^{(l)}$ ，すべての層のパラメータ $\symbf{\Theta}^{(l)}$ はメモリ上に保持する必要がある．それぞれを計算するのに必要な計算量は $O(|\mathcal{E}|), O(L \cdot|\mathcal{V}| \cdot d), O\left(L \cdot d^{2}\right)$ となる．したがって，必要なメモリは合計 $O\left(|\mathcal{E}|+L \cdot|\mathcal{V}| \cdot d+L \cdot d^{2}\right)$ である．グラフが大きいとき，すなわち $|\mathcal{V}|$ や $|\mathcal{E}|$ が大きいときにはメモリに収まらなくなってしまう．さらに，のような計算は効率的ではない．というのも，式(7.1)では必要ないにも関わらず，ラベル付けされていないノード（ $\mathcal{V}_u$ ）の最終的な表現（もしくは $L$ 層目以降の表現）も計算されているからである．詳細に言えば，順方向のプロセスを全エポック行うのに $O\left(L \cdot\left(|\mathcal{E}| \cdot d+|\mathcal{V}| \cdot d^{2}\right)\right)=O\left(L \cdot|\mathcal{V}| \cdot d^{2}\right)$ だけの計算が必要になる．

通常の深層学習では，学習時に必要なメモリを減らす自然なアイデアに確率的勾配降下法（SGD; Stochastic Gradient Descent）を採用していた．これはすべての学習データを使うのではなく，一部の学習データを用いることで勾配を評価するというものである．しかし，グラフ構造のデータにSGDを用いるのは他の深層学習の場合ほど簡単ではない．なぜなら，の学習データは，グラフ内の他の学習データとつながっているからである．つまり，ノード $v_i$ についての損失 $\ell\left(f_{\text{GCN}}(\symbf{A}, \symbf{F} ; \symbf{\Theta})_i, y_i\right)$ を計算するためには，他のたくさんのノード表現が関係することがのグラフフィルタリングの仕組みからわかる．

たくさんのノードが関係してくることをより具体的に理解するために，ノード $v_i$ に注目してを以下のように局所的な視点で捉えてみる：

\[\tag{7.4} \symbf{F}_i^{(l)}=\sum_{v_j \in \widetilde{\mathcal{N}}\left(v_i\right)} \hat{\symbf{A}}_{i, j} \symbf{F}_j^{(l-1)} \symbf{\Theta}^{(l-1)}, \quad l=1, \ldots, L\]

これは周辺ノードの情報を集約している形になっている．なお， $l$ 番目のグラフフィルタ層を経たノード $v_i$ のノード表現を $\symbf{F}_i^{(l)}$ と書く．また， $\hat{\symbf{A}}_{i, j}$ は $\hat{\symbf{A}}$ の $(i,j)$ 要素であり， $\widetilde{\mathcal{N}}\left(v_i\right)=\mathcal{N}\left(v_i\right) \cup\left\{v_i\right\}$ はノード $v_i$ 自身を含んだ近傍ノードの集合を表す．

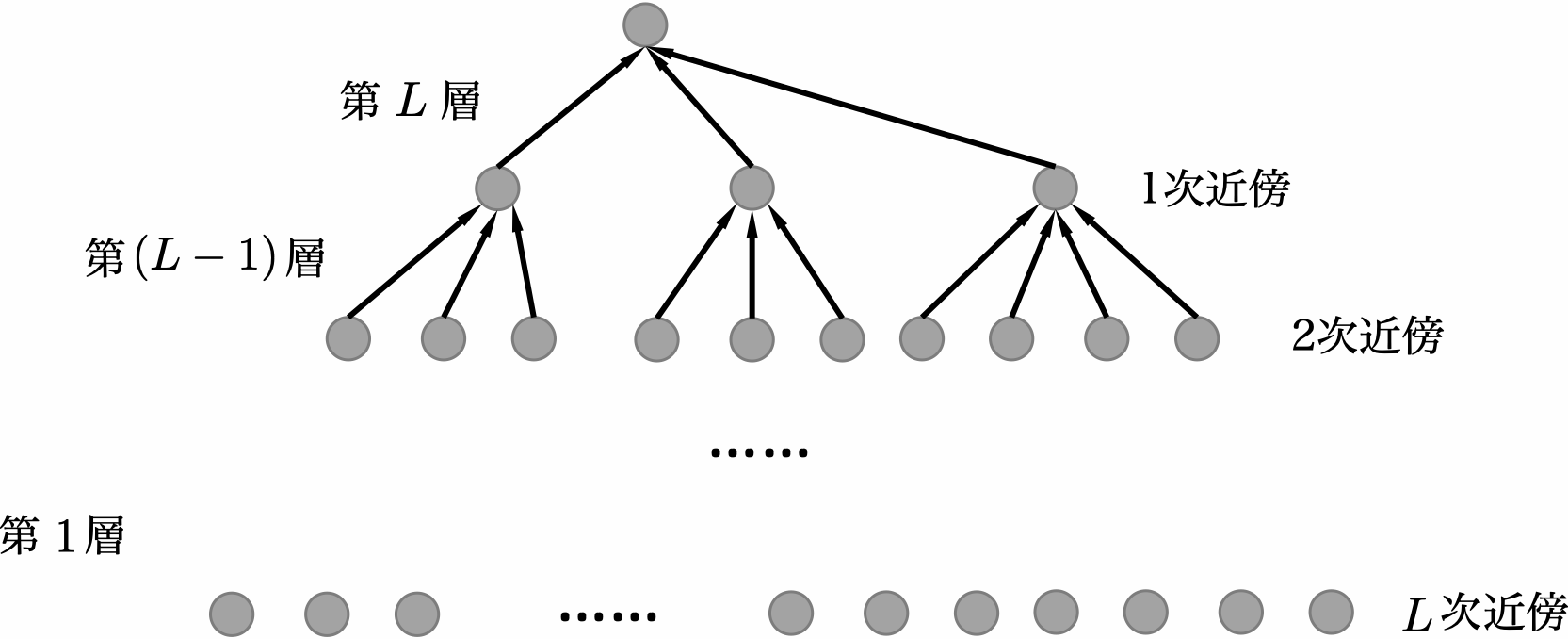
したがって，図7.1のように $L$ 層目から入力層にかけてみていくと， $L$ 層目のグラフフィルタ層（出力層）のノード $v_i$ の表現を計算するためには，近傍ノード（自身を含む）の $L-1$ 層目の表現が必要になる．ノード $v_j \in \widetilde{\mathcal{N}}\left(v_i\right)$ の $L-1$ 層目の表現を計算するためには，それらの近傍ノードの $L-2$ 層目の表現が必要になる．全ノードの $\widetilde{\mathcal{N}}\left(v_i\right)$ における近傍ノードは，ノード $v_i$ の「近傍の近傍」，すなわちノード $v_i$ の2次近傍になる．

一般的に，ノード $v_i$ の損失を計算するためには $L$ 層後のノード $v_i$ の表現とその $l$ 次近傍の表現が必要であり，その $l$ 次近傍の表現は $L-l+1$ 番目のグラフフィルタ層によって要求されることになる（図7.1）．具体的には， $L$ 次近傍ノードの表現は入力層（1層目）のグラフフィルタ層によって要求されることになる．したがって，計算全体では，ノード $v_i$ の $L$ 次近傍までの全ノードが関与することにより，ノード $v_i$ の損失は次のように書き直すことができる：

\[\tag{7.5} \ell\left(f_{\text{GCN}}(\symbf{A}, \symbf{F} ; \symbf{\Theta})_i, y_i\right)=\ell\left(f_{\text{GCN}}\left(\symbf{A}\left\{\mathcal{N}^{L}\left(v_i\right)\right\}, \symbf{F}\left\{\mathcal{N}^{L}\left(v_i\right)\right\} ; \symbf{\Theta}\right), y_i\right)\]

ここで， $\mathcal{N}^{L}\left(v_i\right)$ は，ノード $v_i$ から $L$ 次以内にあるノード集合を表す（図7.1の全ノードに対応）． $\symbf{A}\left\{\mathcal{N}^{L}\left(v_i\right)\right\}$ は， $\mathcal{N}^{L}\left(v_i\right)$ に対応する隣接行列の行と列を取り出した行列である． $\symbf{F}\left\{\mathcal{N}^{L}\left(v_i\right)\right\}$ は $\mathcal{N}^{L}\left(v_i\right)$ に対応するノードの入力表現を表す．パラメータ更新にはミニバッチ確率的勾配降下法(SGD)が使われることが多い（ $\mathcal{V}_l$ から小グループのデータ（ミニバッチ）を選んで勾配を推計する）．ミニバッチごとの損失関数は次のように表すことができる：

\[\tag{7.6} \mathcal{L}_{\mathcal{B}}=\sum_{v_i \in \mathcal{B}}\ell\left(f_{\text{GCN}}\left(\symbf{A}\left\{\mathcal{N}^{L}\left(v_i\right)\right\}, \symbf{F}\left\{\mathcal{N}^{L}\left(v_i\right)\right\} ; \symbf{\Theta}\right), y_i\right)\]

ここで， $\mathcal{B} \subset \mathcal{V}_l$ はサンプリングされたミニバッチである．

しかしながら，最適化にSGDを使った場合でも依然として多くのメモリが必要になる．図7.1からわかるように，グラフフィルタ層 $L$ が増えるとノード集合 $\mathcal{N}^{L}\left(v_i\right)$ は指数関数的に増えてしまうことが大きな問題となる． $\mathcal{N}^{L}\left(v_i\right)$ のノード数のオーダーは $deg^{L}$ （ $deg$ はグラフの平均次数）となることから，SGDを使った最適化を行うためには，ノード表現の保持に $O\left(d e g^{L} \cdot d\right)$ だけのメモリが必要になる．さらに実際の運用では，平均的なデータ量のミニバッチを基準にするのではなく，最もメモリ使用量が多くなるような「最悪のケース」のミニバッチに対して十分なメモリを用意する必要がある．つまり，ミニバッチ内に大きな次数を持つノードが存在する場合，多くの他のノードが関与することになり，かなりの量のメモリが必要になってしまう．この「近傍ノードの数が指数関数的に増えていく」問題は近傍膨張もしくは近傍爆発と呼ばれる(Chen et al., 2018a, b; Huang et al., 2018)．なお， $L$ がグラフの直径よりも大きいときには， $\mathcal{N}^{L}\left(v_i\right)=\mathcal{V}$ となるので，これは全ノード集合が計算に必要になることを意味し，近傍爆発の極端なケースになる．

近傍爆発問題は他にもSGD法の時間効率にも影響を与えている．具体的に見積もると，ノード $v_i$ についての最終的な表現 $\symbf{F}_i^{(L)}$ を計算するための時間計算量は $O\left(deg^{L} \cdot\left(\operatorname{deg} \cdot d+d^{2}\right)\right)$ である．ただしグラフの平均次数 $deg$ は通常 $d$ （表現の次元）よりも十分小さいので，これは $O\left(d e g^{L} \cdot d^{2}\right)$ となる．次に，学習データ $\mathcal{V}_l$ 全体を1エポック走らせるのにかかる時間計算量は $O\left(\left|\mathcal{V}_l\right| \cdot \mathrm{deg}^{L} \cdot d^{2}\right)$ である．ここでは，各ミニバッチが単一の学習データのみを含むと仮定している．なお，バッチサイズ $|\mathcal{B}|$ が1より大きい場合，エポックごとの時間計算量は抑えられる．というのも，この場合には各ミニバッチ $\mathcal{B}$ に含まれるノード一部がいくつかのサンプル $v_i$ の $\widetilde{\mathcal{N}}^{L}(v_i)$ に存在し，その表現が計算中に共有されるためである．ラベル付されていないノードの最終的な表現が計算されないにもかかわらず， $L$ が大きい場合， $O\left(L\cdot |\mathcal{V}|\cdot d^2\right)$ が必要となる全学習データを使った勾配法と比較して，SGDの時間計算量は（ $deg^{L}$ が効いてくるため）より高くなる可能性がある．

GCNフィルタを用いたGNNモデルにおける「近傍爆発」の問題を紹介したが，この問題は式(7.4)のように近傍ノードの情報を集約するプロセスがある限り他のグラフフィルタでも起きる．よって本章では，一般性を失わない形で，GCNフィルタに基づいて議論と分析を行っている． GNNモデルのスケーラビリティを改善し，「近傍爆発」問題を解決するため，様々な近傍ノードのサンプリング手法が提案されている．これらの手法の主な目的は，式(7.6)の計算に関わるノード数を減らし，それによって必要とされる計算時間とメモリを削減することである．サンプリングの方法には3つの主要な方法がある：

ノードサンプリング

ノードの表現を計算する際に，各層において近傍ノードからノードをサンプリングする（すべての近傍ノードを計算に用いない）方法．近傍のすべての情報を集約するのではなく，サンプリングされたノードにのみ基づいてノード表現を計算する．
層サンプリング

各層ごとに計算に用いるノードを固定する方法（異なる層では異なるノード集合を用い得る）．言い換えると，ノード $v_i$ と $v_j$ に関する $\symbf{F}_i^{(l)}$ と $\symbf{F}_j^{(l)}$ を計算するために，同じサンプリングされたノード集合を用いる方法である．ノードサンプリングでも解決できない近傍爆発の問題を解決されるために提案された．
部分グラフサンプリング

元のグラフから部分グラフをサンプリングし，その部分グラフを元にノード表現を学習する方法．

本章では，各サンプリングの方法について代表的なアルゴリズムを紹介する．

グラフ深層学習

グラフニューラルネットワーク（GNN）の入門書

第7章 GNNのスケーラビリティ

はじめに

目次