第5章 グラフニューラルネットワーク
はじめに
グラフニューラルネットワーク(GNN)は,グラフ構造を持つデータに対して深層ニューラルネットワークを適用するものである. グラフは一定のパターンを持つ構造ではないため,従来の深層ニューラルネットワークをグラフ構造を持つデータに一般化することは容易ではない. グラフニューラルネットワークの研究は,21世紀初頭に最初のGNNモデル(Scarselli et al., 2005, 2008)が提案されたことが始まりとされる. そこではノードおよびグラフを対象としたタスクの両方に対してGNNが提案された. 深層学習技術が画像処理や自然言語処理などの幅広い分野で大きな人気を博すようになると,多くの研究者はこの研究分野に力を注ぐようになった.
グラフニューラルネットワークは,グラフの特徴量学習の一過程として捉えることができる. ノードを対象としたタスクでは,GNNは各ノードの優れた特徴を学習し,タスクの実行を容易にすることを目標にしている. グラフを対象としたタスクでは,GNNはグラフ全体を代表する特徴を学習することを目標としており,このタスクにおいてはノードの特徴の学習は,グラフ全体を学習するための中間的なステップとなる. ノードの特徴を学習する過程では,入力ノードの特徴とグラフ構造の両方を活用することが多い. 具体的にこのプロセスは,以下のようにまとめることができる:
\[\tag{5.1} \symbf{F}^{(\mathrm{of})}=h\left(\symbf{A}, \symbf{F}^{(\mathrm{if})}\right)\]ここで, $\symbf{A} \in \mathbb{R}^{N \times N}$ は(グラフの構造に相当する)ノード数 $N$ 個のグラフの隣接行列を表し, $\symbf{F}^{(\text{if})} \in \mathbb{R}^{N \times d_{\mathrm{if}}}$ と $\symbf{F}^{(\text{of})} \in \mathbb{R}^{N \times d_{\text {of}}}$ は,それぞれ入力特徴量行列(入力表現行列)と出力特徴量行列(出力表現行列)を表す( $d_{\text{if}}$ と $d_{\text{of}}$ は,それぞれ入力と出力におけるノードが持つ特徴の次元を表す). 本書では一般に,ノードの特徴とグラフ構造を入力とし,新しいノードの特徴の集合を出力する処理を,グラフフィルタリングと呼ぶことにする. 図5.1中の上付き文字(または下付き文字)にある”if”と”of”は,それぞれフィルタリングの入力(input of filtering)と出力(output of filtering)を表している. また,演算子 $h(\cdot,\, \cdot)$ をグラフフィルタと呼ぶ. 図5.1は典型的なグラフフィルタリングを示しいる.グラフフィルタリングはグラフ構造を変えず,ノードの特徴のみを更新する.
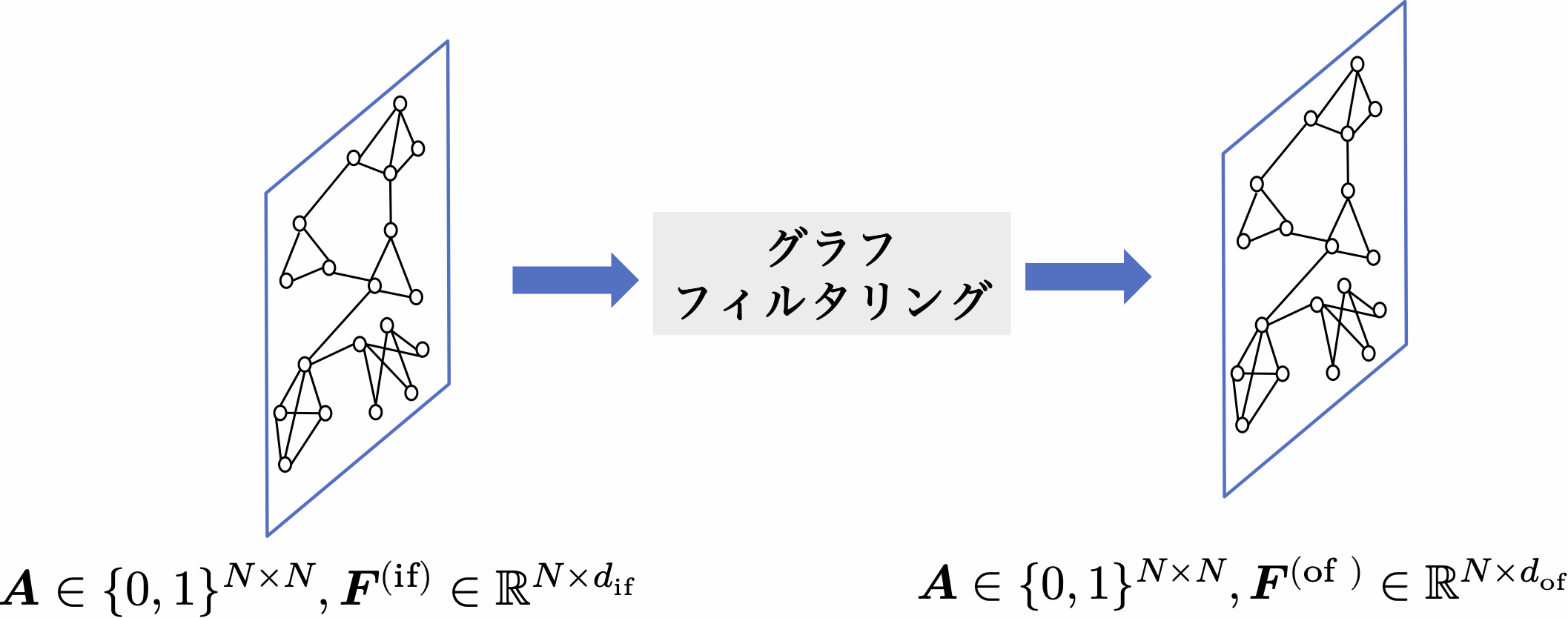
ノードを対象としたタスクでは,グラフフィルタリングだけで十分であり,通常は複数のグラフフィルタリングを連続的に積み重ねることで最終的なノードの表現を生成する. しかし,グラフを対象としたタスクでは,ノード表現からグラフ全体の表現を生成するために別の操作が必要になる. そこで,従来のCNNと同様に,ノードの表現を集約しグラフ全体の表現を生成するようなプーリングが提案されている. 従来のCNNは(画像データのような)規則正しいグリッド上に存在するデータに適用される. しかし,グラフ構造は不規則であるため,グラフニューラルネットワーク専用のプーリングが必要となる. グラフプーリングの多くはグラフを入力として受け取り,ノード数の少ない粗化グラフ(coarsened graph)を生成する.
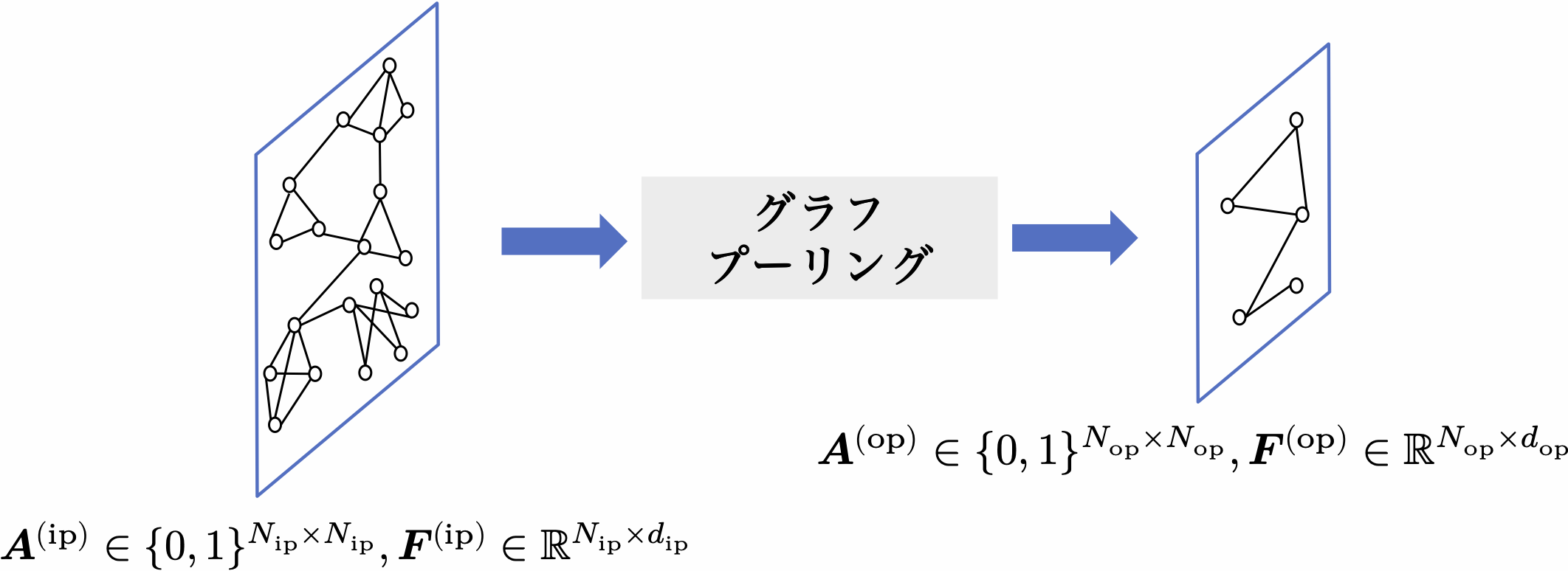
したがって,グラフプーリングの肝は,粗化グラフの構造情報(つまり隣接行列)とその粗化グラフ内のノードの表現を生成することとなる. 一般に,図5.2に示すように,グラフプーリング操作は以下のように記述することができる.
\[\tag{5.2} \symbf{A}^{(\mathrm{op})}, \symbf{F}^{(\mathrm{op})}=\operatorname{pool}\left(\symbf{A}^{(\mathrm{ip})}, \symbf{F}^{(\mathrm{ip})}\right)\]ここで, $\symbf{A}^{(\mathrm{ip})} \in \mathbb{R}^{N_{\mathrm{ip}} \times N_{\mathrm{ip}}}$ と $\symbf{F}^{(\mathrm{ip})} \in \mathbb{R}^{N_{\mathrm{ip}} \times d_{\mathrm{ip}}}$ ,そして $\symbf{A}^{(\mathrm{op})} \in \mathbb{R}^{N_{\mathrm{op}} \times N_{\mathrm{op}}}$ と $\symbf{F}^{(\mathrm{op})} \in \mathbb{R}^{N_{\mathrm{op}} \times d_{\mathrm{op}}}$ はそれぞれ,プーリング前後の隣接行列と特徴量行列を表す. また,上付き文字(または下付き文字)”ip”と “op”はそれぞれ,プーリングの入力(input of pooling)と出力(output of pooling)を表す. なお,粗化グラフのノード数 $N_{\mathrm{op}}$ に対しては, $N_{\mathrm{op}}<N_{\mathrm{ip}}$ を満たすことになる.
一般的なグラフニューラルネットワークモデルは,グラフフィルタリングとグラフプーリングのどちらか一方,または両方から構成されている. ノードを対象としたタスクの場合,GNNはグラフフィルタリングのみを利用する. この場合,グラフフィルタリング層を複数積み重ね,前の層の出力が次の層の入力となるような構成が一般的である. 一方グラフを対象としたタスクの場合,GNNはグラフフィルタリングとグラフプーリングの両方を必要とする. この場合,グラフフィルタリング層をいくつかのブロックに分割し,それぞれのブロックの間にグラフプーリング層が挿入されることが多い. 本章では,まずGNNの一般的な構成を簡単に紹介し,次に代表的なグラフフィルタリングおよびグラフプーリングの詳細を説明していく.
目次
- 5.1 はじめに
- 5.2 一般的な GNN のフレームワーク
- 5.2.1 ノードを対象としたタスクのフレームワーク
- 5.2.2 グラフを対象としたタスクのフレームワーク
- 5.3 グラフフィルタ
- 5.3.1 スペクトル型グラフフィルタ
- 5.3.1.1 グラフの周波数フィルタリング
- 5.3.1.2 スペクトル型グラフフィルタ
- 5.3.1.3 チェビシェフ多項式とチェビシェフフィルタ
- 5.3.1.4 GCN フィルタ:単純化された 1 次のチェビシェフフィルタ
- 5.3.1.5 複数チャンネルのグラフ信号に対するグラフフィルタ
- 5.3.2 空間型グラフフィルタ
- 5.3.2.1 最初期のグラフニューラルネットワーク (GNN) のフィルタ
- 5.3.2.2 GraphSAGE フィルタ
- 5.3.2.3 GAT フィルタ
- 5.3.2.4 ECC フィルタ
- 5.3.2.5 GGNN フィルタ
- 5.3.2.6 Mo フィルタ
- 5.3.2.7 MPNN(空間型グラフフィルタの一般的なフレームワーク)
- 5.3.1 スペクトル型グラフフィルタ
- 5.4 グラフプーリング
- 5.4.1 平坦グラフプーリング
- 5.4.2 階層的グラフプーリング
- 5.4.2.1 ダウンサンプリング型プーリング
- 5.4.2.2 スーパーノード型プーリング
- 5.5 GNN の学習
- 5.5.1 ノード分類における学習
- 5.5.2 グラフ分類における学習
- 5.6 本章のまとめ
- 5.7 参考文献