第4章 グラフ埋め込み
はじめに
グラフ埋め込み(Graph Embedding)は,与えられたグラフの各ノードを低次元ベクトル表現(これらのベクトルを一般的にノード埋め込みと言う)に写像することを目指している. この写像は,元のグラフ内のノードが持つ重要な情報を保存するように行われる. グラフ内のノードは,次の2つのドメイン(領域)で表現することができる.
- グラフドメイン:エッジの繋がり(グラフ構造)によってノードを表現
- 埋め込みドメイン:連続値を要素に持つベクトルによってノードを表現
以上 (2) つのドメインを考慮すると,グラフ埋め込みは,グラフドメインの情報が埋め込みドメインでも保存されるように,各ノードをグラフドメインから埋め込みドメインへ写像することを目指している. するとここで,2つの重要な疑問が浮かんでくる.
- どんな情報を保存する必要があるのか?
- どのようにその情報を保存するのか?
ほとんどの場合,グラフ埋め込みのアルゴリズムが異なれば,この2つの問いに対する答えは変わってくるだろう. 最初の問いにある「保存する情報」については,ノードの近傍情報(Perozzi et al., 2014; Tang et al., 2015; Grover and Leskovec, 2016)や,ノードの構造的な役割(Ribeiro et al., 2017),ノードの状態(Ma et al., 2017; Lai et al., 2017; Gu et al., 2018),コミュニティ情報(Wang et al., 2017c)など,多くの種類の情報が保存の対象として研究されている. 2つ目の問いに対しても,様々な手法が提案されている. 技術的な詳細は手法によって異なるが,ほとんどの手法は「埋め込みドメインのノード表現を用いて,保存すべきグラフドメインの情報を再構成する」という点で共通している. 優れたノード表現というのは,保存したい情報を再構成できるはずである. したがって,再構成誤差(reconstruction error)を最小にすることで,グラフドメインから埋め込みドメインへの写像を学習することを目指すことになる. グラフ埋め込みの一般的なプロセスをまとめるために,図4.1に全体的なフレームワークを示した.
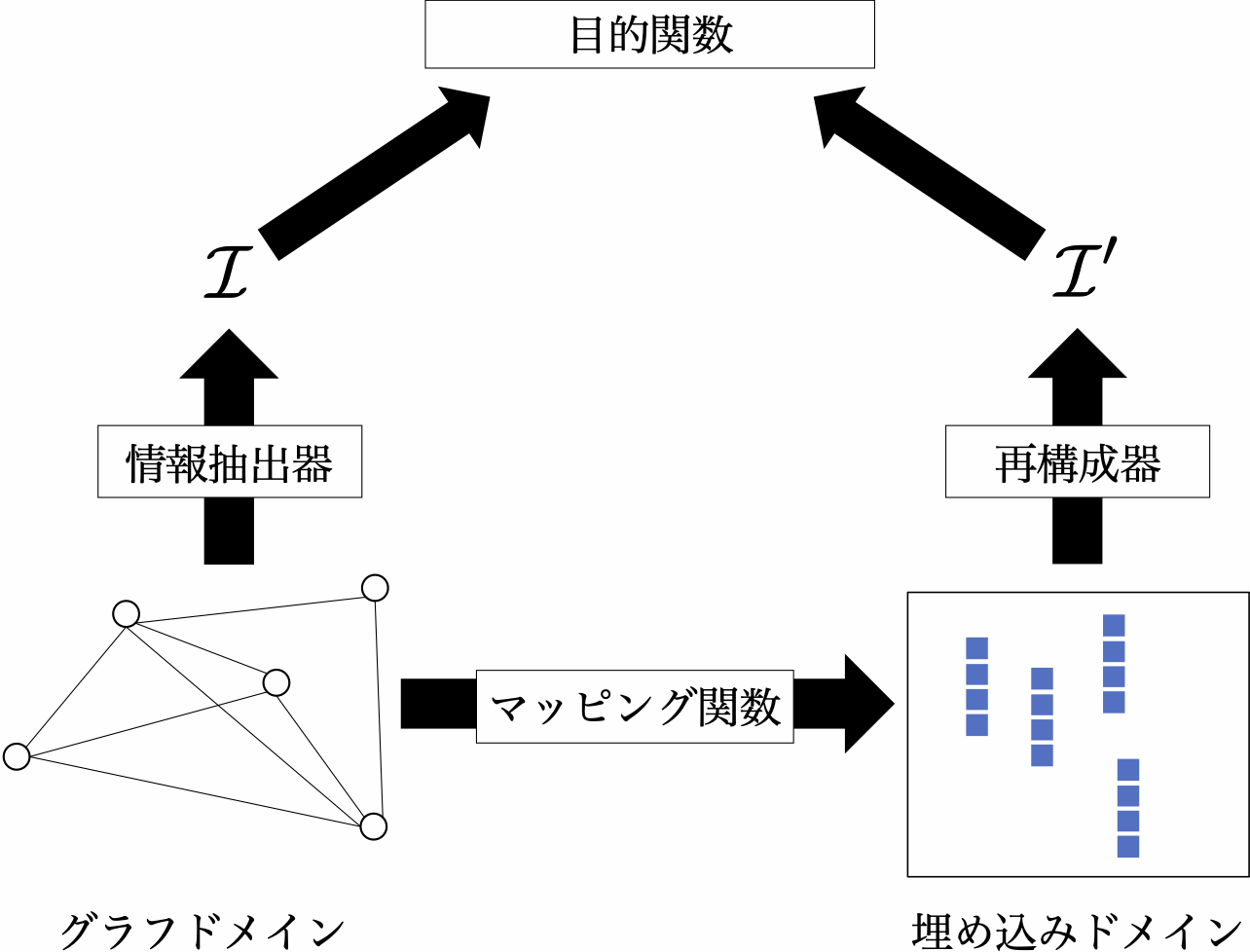
図4.1に示されているように,この一般的なフレームワークは4つの重要な要素で構成される.
- マッピング関数(Mapping):グラフドメインから埋め込みドメインへ,ノードを写像する関数
- 情報抽出器(Extractor):グラフドメインから保存したい重要な情報 (\mathcal{I}) を抽出する
- 再構成器(Reconstructor):埋め込みドメインの埋め込み情報を使って,抽出されたグラフ情報 (\mathcal{I}) を再構成する.なお,図4.1に示すように,再構成された情報は (\mathcal{I}^{\prime}) と表記される.
- 目的関数(Objective):目的関数は,抽出された情報 (\mathcal{I}) と再構成された情報 (\mathcal{I}^{\prime}) を基に作成される.一般的に,マッピング関数や再構成に関係する全パラメータを学習するために,この目的関数を最適化することになる.
本章では,図4.1の一般的なフレームワークに沿って,グラフドメインが持つ様々な種類の情報を保存する代表的なグラフ埋め込み手法を紹介する. その後,ヘテログラフや二部グラフ,多次元グラフ,符号付きグラフ,ハイパーグラフ,ダイナミックグラフに特化したグラフ埋め込みアルゴリズムを紹介する.
目次
- 4.1 はじめに
- 4.2 単純グラフのグラフ埋め込み
- 4.2.1 ノード共起性の保存
- 4.2.1.1 マッピング関数
- 4.2.1.2 ランダムウォークに基づく共起性の抽出
- 4.2.1.3 共起性の再構成および目的関数
- 4.2.1.4 学習過程の高速化
- 4.2.1.5 階層的ソフトマックス
- 4.2.1.6 ネガティブサンプリング
- 4.2.1.7 実際の学習プロセスについて:バッチ処理
- 4.2.1.8 共起性を保存するその他の手法
- 4.2.1.9 node2vec
- 4.2.1.10 LINE
- 4.2.1.11 行列分解による表示
- 4.2.2 構造的役割の保存
- 4.2.2.1 構造類似性の測定
- 4.2.2.2 構造類似性に基づくグラフの生成
- 4.2.2.3 多層グラフ上での偏りのあるランダムウォーク
- 4.2.3 ノード状態の保存
- 4.2.3.1 情報抽出
- 4.2.3.2 再構成
- 4.2.4 コミュニティ構造の保存
- 4.2.4.1 ノード指向構造の保存
- 4.2.4.2 ノード指向構造の保存:情報抽出
- 4.2.4.3 ノード指向構造の保存:再構成および目的関数
- 4.2.4.4 コミュニティ構造の保存
- 4.2.4.5 全体の目的関数
- 4.2.1 ノード共起性の保存
- 4.3 複雑グラフ上のグラフ埋め込み
- 4.3.1 ヘテログラフの埋め込み
- 4.3.1.1 メタパスに基づく情報抽出
- 4.3.1.2 再構成
- 4.3.2 二部グラフの埋め込み
- 4.3.2.1 情報抽出
- 4.3.2.2 再構成および目的関数
- 4.3.3 多次元グラフの埋め込み
- 4.3.3.1 マッピング関数
- 4.3.3.2 情報抽出
- 4.3.3.3 再構成および目的関数
- 4.3.4 符号付きグラフの埋め込み
- 4.3.4.1 情報抽出
- 4.3.4.2 再構成
- 4.3.4.3 目的関数
- 4.3.5 ハイパーグラフの埋め込み
- 4.3.5.1 情報抽出
- 4.3.5.2 マッピング関数
- 4.3.5.3 再構成および目的関数
- 4.3.6 ダイナミックグラフの埋め込み
- 4.3.6.1 情報抽出
- 4.3.1 ヘテログラフの埋め込み
- 4.4 本章のまとめ
- 4.5 参考文献